Chapter 14 : Graphs, Geometry, and Geographic Information Systems

In this chapter, we will cover the following topics:

In this chapter, we will cover Python's capabilities in graph theory, geometry, and geography.

Graphs are mathematical objects describing relations between items. They are ubiquitous in science and engineering, as they can represent many kinds of real-world relations: friends in a social network, atoms in a molecule, website links, cells in a neural network, neighboring pixels in an image, and so on. Graphs are also classical data structures in computer science. Finally, many domain-specific problems may be re-expressed as graph problems, and then solved with well-known algorithms.

We will also see a few recipes related to geometry and Geographic Information Systems (GIS), which refers to the processing and analysis of any kind of spatial, geographical, or topographical data.

In this introduction, we will give a brief overview of these topics.

Graphs

Mathematically, a graph \(G = (V, E)\) is defined by a set \(V\) of vertices or nodes, and a set \(E\) of edges (two-element subsets of \(V\)). Two nodes \(v\) and \(v'\) are said to be connected if \((v, v')\) is an edge (element of \(E\)).

  • If the edges are unordered (meaning that \((v,v') = (v',v)\)), the graph is said to be undirected
  • If the edges are ordered (meaning that \((v,v') \neq (v',v)\)), the graph is said to be directed

An edge in an undirected graph is represented by a line segment between the two nodes. In a directed graph, it is represented by an arrow.

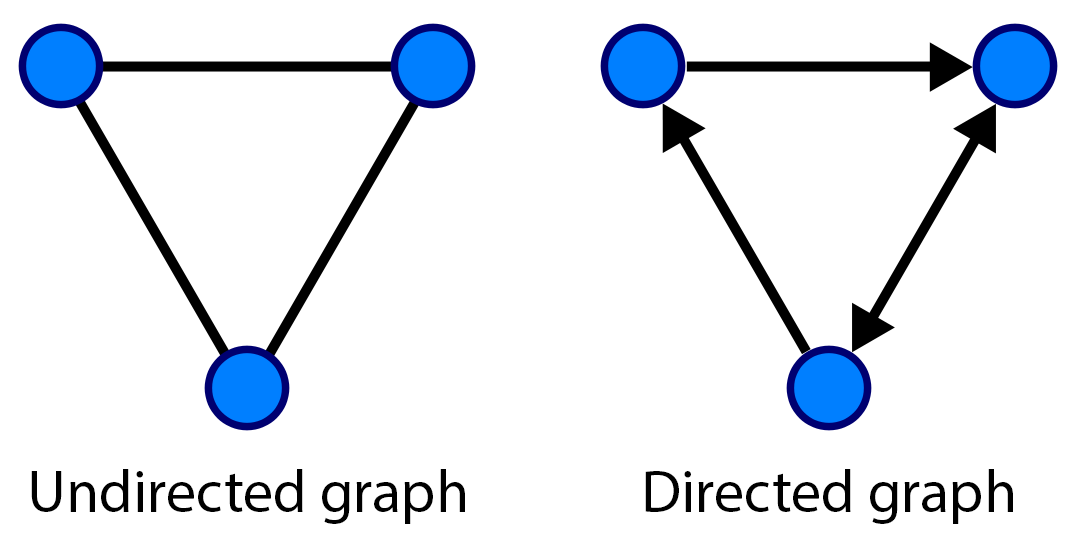
Undirected and directed graphs

A graph can be represented by different data structures, such as an adjacency list (for each vertex, a list of adjacent vertices) or an adjacency matrix (matrix of connections between vertices).

Problems in graph theory

Here are a few examples of classical graph problems:

Random graphs

Random graphs are particular kinds of graphs defined with probabilistic rules. They are useful for understanding the structure of large real-world graphs such as social graphs.

In particular, small-world networks have sparse connections, but most nodes can be reached from every other node in a small number of steps. This property is due to the existence of a small number of hubs that have a high number of connections.

Graphs in Python

Although graphs can be manipulated with native Python structures, it is more convenient to use a dedicated library implementing specific data structures and manipulation routines. In this chapter, we will use NetworkX, a pure Python library. An alternative library is graph-tool, largely written in C++.

NetworkX implements a flexible data structure for graphs, and it contains many algorithms. NetworkX also lets us draw graphs easily with matplotlib.

Geometry in Python

Shapely is a Python library used to manipulate 2D geometrical shapes such as points, lines, and polygons. It is most notably useful in Geographic Information Systems.

Geographical Information Systems in Python

There are several Python modules used to manipulate geographical data and plotting maps.

In this chapter, we will use cartopy and Shapely to handle GIS files.

The ESRI shapefile is a popular geospatial vector data format. It can be read by cartopy and NetworkX.

Cartopy is a Python library that provides cartographic tools for Python. We can use it to perform map projections and draw maps with matplotlib. It relies on Shapely.

geoplot is a young high-level geospatial data visualization library in Python that builds on top of cartopy and matplotlib.

We will also use the OpenStreetMap service, a free, open source, collaborative service providing maps of the world.

Other GIS/mapping systems in Python that we couldn't cover in this chapter include GeoPandas and Kartograph.

References

Here are a few references about graphs:

Here are a few references about geometry and maps in Python: