14.3. Resolving dependencies in a directed acyclic graph with a topological sort

IPython Cookbook, Second Edition This is one of the 100+ free recipes of the IPython Cookbook, Second Edition, by Cyrille Rossant, a guide to numerical computing and data science in the Jupyter Notebook. The ebook and printed book are available for purchase at Packt Publishing.

▶  Text on GitHub with a CC-BY-NC-ND license
▶  Code on GitHub with a MIT license

▶  Go to Chapter 14 : Graphs, Geometry, and Geographic Information Systems
▶  Get the Jupyter notebook

In this recipe, we will show an application of a well-known graph algorithm: topological sorting. Let's consider a directed graph describing dependencies between items. For example, in a package manager, before we can install a given package P, we may need to install dependent packages.

The set of dependencies forms a directed graph. With topological sorting, the package manager can resolve the dependencies and find the right installation order of the packages.

Topological sorting has many other applications. Here, we will illustrate this notion on real data from the JavaScript package manager npm. We will find the installation order of the required packages for the react JavaScript package.

How to do it...

1.  We import a few packages:

import io
import json
import requests
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
%matplotlib inline

2.  We download the dataset (a GraphML file stored on GitHub, that we created using a script at https://github.com/graphcommons/npm-dependency-network) and we load it with the NetworkX function read_graphml():

url = ('https://github.com/ipython-books/'
       'cookbook-2nd-data/blob/master/'
       'react.graphml?raw=true')
f = io.BytesIO(requests.get(url).content)
graph = nx.read_graphml(f)

3.  The graph is a directed graph (DiGraph) with few nodes and edges:

graph

<networkx.classes.digraph.DiGraph at 0x7f69ac6dfdd8>

len(graph.nodes), len(graph.edges)

(16, 20)

4.  Let's draw this graph:

fig, ax = plt.subplots(1, 1, figsize=(8, 8))
nx.draw_networkx(graph, ax=ax, font_size=10)
ax.set_axis_off()

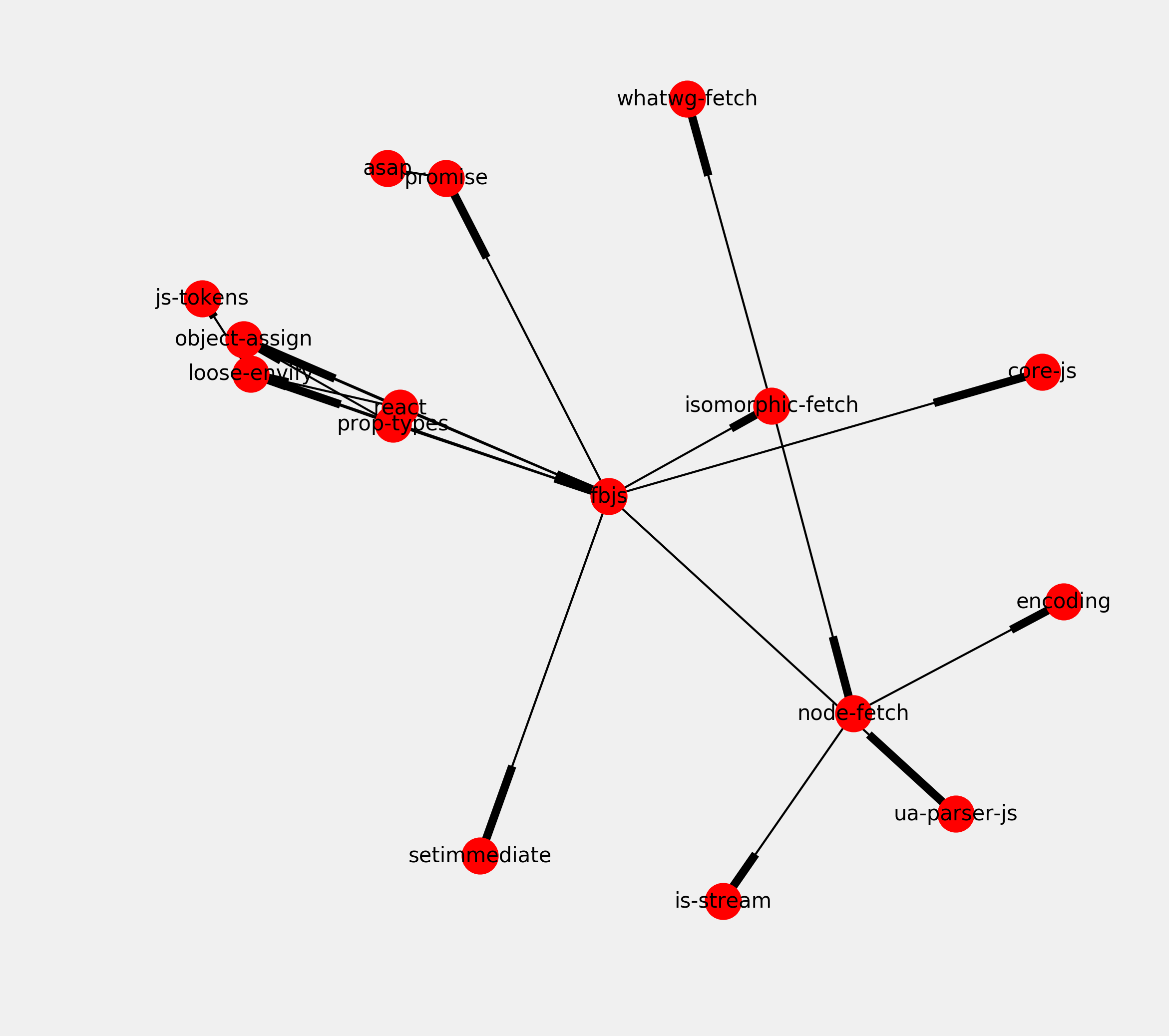
<matplotlib.figure.Figure at 0x7f69b4af1a58>

5.  A topological sort only exists when the graph is a directed acyclic graph (DAG). This means that there is no cycle in the graph, that is, no circular dependency. Is our graph a DAG? Let's see:

nx.is_directed_acyclic_graph(graph)

True

6.  We can perform the topological sort, thereby obtaining a linear installation order satisfying all dependencies:

ts = list(nx.topological_sort(graph))
ts

['react',
 'prop-types',
 'fbjs',
 'ua-parser-js',
 'setimmediate',
 'promise',
 'asap',
 'object-assign',
 'loose-envify',
 'js-tokens',
 'isomorphic-fetch',
 'whatwg-fetch',
 'node-fetch',
 'is-stream',
 'encoding',
 'core-js']

Since we used the convention that A directs to B if B needs to be installed before A (A depends on B), the installation order is the reversed order here.

7.  Finally, we draw our graph with a shell layout algorithm, and we display the dependence order using the node colors (darker nodes need to be installed before lighter ones):

# Each node's color is the index of the node in the
# topological sort.
colors = [ts.index(node) for node in graph.nodes]

nx.draw_shell(graph,
              node_color=colors,
              cmap=plt.cm.Blues,
              font_size=8,
              width=.5
              )

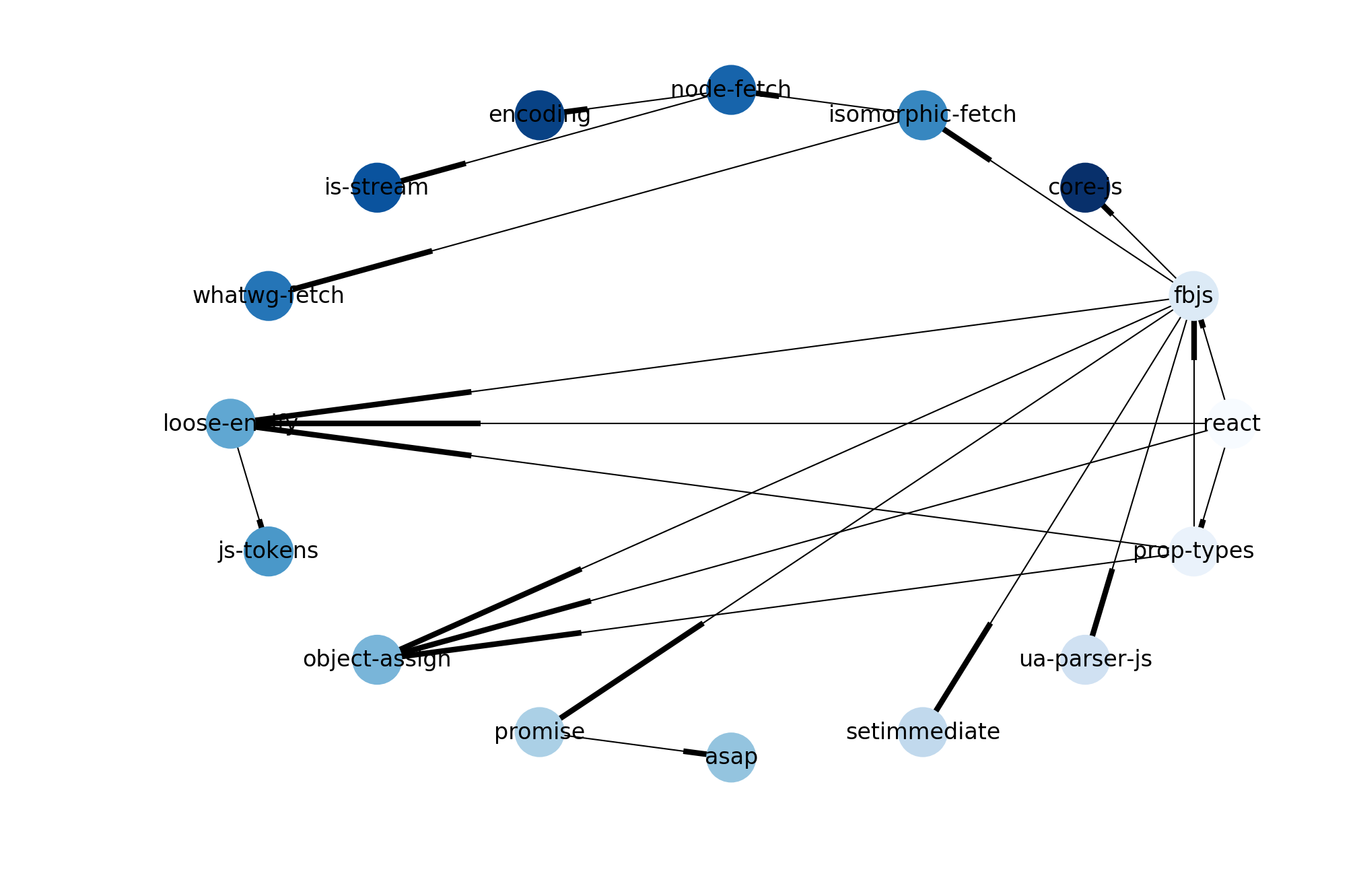
<matplotlib.figure.Figure at 0x7f69ac59f400>

How it works...

We used the following code (adapted from https://github.com/graphcommons/npm-dependency-network) to obtain the dependency graph of the react npm package:

from lxml.html import fromstring
import cssselect  # Need to do: pip install cssselect
from requests.packages import urllib3

urllib3.disable_warnings()
fetched_packages = set()

def import_package_dependencies(graph, pkg_name,
                                max_depth=3, depth=0):
    if pkg_name in fetched_packages:
        return
    if depth > max_depth:
        return
    fetched_packages.add(pkg_name)
    url = f'https://www.npmjs.com/package/{pkg_name}'
    response = requests.get(url, verify=False)
    doc = fromstring(response.content)
    graph.add_node(pkg_name)
    for h3 in doc.cssselect('h3'):
        content = h3.text_content()
        if content.startswith('Dependencies'):
            for dep in h3.getnext().cssselect('a'):
                dep_name = dep.text_content()
                print('-' * depth * 2, dep_name)
                graph.add_node(dep_name)
                graph.add_edge(pkg_name, dep_name)
                import_package_dependencies(
                    graph,
                    dep_name,
                    depth=depth + 1
                )

graph = nx.DiGraph()
import_package_dependencies(graph, 'react')
nx.write_graphml(graph, 'react.graphml')

You can use that code to obtain the dependency graph of any other npm package. The script may take a few minutes to complete.

There's more...

Directed acyclic graphs are found in many applications. They can represent causal relations, influence diagrams, dependencies, and other concepts. For example, the version history of a distributed revision control system such as Git is described with a DAG.

Topological sorting is useful in any scheduling task in general (project management and instruction scheduling).

Here are a few references: