15.3. Analyzing real-valued functions

IPython Cookbook, Second Edition This is one of the 100+ free recipes of the IPython Cookbook, Second Edition, by Cyrille Rossant, a guide to numerical computing and data science in the Jupyter Notebook. The ebook and printed book are available for purchase at Packt Publishing.

▶  Text on GitHub with a CC-BY-NC-ND license
▶  Code on GitHub with a MIT license

▶  Go to Chapter 15 : Symbolic and Numerical Mathematics
▶  Get the Jupyter notebook

SymPy contains a rich calculus toolbox to analyze real-valued functions: limits, power series, derivatives, integrals, Fourier transforms, and so on. In this recipe, we will show the very basics of these capabilities.

How to do it...

1.  Let's define a few symbols and a function (which is just an expression depending on x):

from sympy import *
init_printing()

var('x z')

(x, z)

f = 1 / (1 + x**2)

2.  Let's evaluate this function at 1:

f.subs(x, 1)

1/2

3.  We can compute the derivative of this function:

diff(f, x)

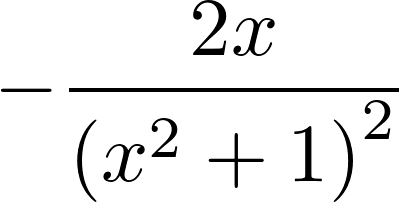
Output

4.  What is \(f\)'s limit to infinity? (Note the double o (oo) for the infinity symbol):

limit(f, x, oo)

0

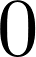
5.  Here's how to compute a Taylor series (here, around 0, of order 9). The Big O can be removed with the removeO() method.

series(f, x0=0, n=9)

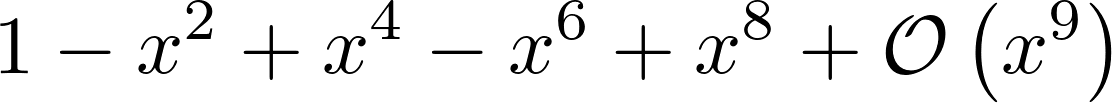
Output

6.  We can compute definite integrals (here, over the entire real line):

integrate(f, (x, -oo, oo))

Pi

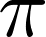
7.  SymPy can also compute indefinite integrals:

integrate(f, x)

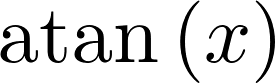
atan(x)

8.  Finally, let's compute \(f\)'s Fourier transforms:

fourier_transform(f, x, z)

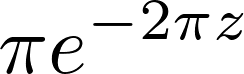
Output

There's more...

SymPy includes a large number of other integral transforms besides the Fourier transform (http://docs.sympy.org/latest/modules/integrals/integrals.html). However, SymPy will not always be able to find closed-form solutions.

Here are a few general references about real analysis and calculus: