15.2. Solving equations and inequalities

IPython Cookbook, Second Edition This is one of the 100+ free recipes of the IPython Cookbook, Second Edition, by Cyrille Rossant, a guide to numerical computing and data science in the Jupyter Notebook. The ebook and printed book are available for purchase at Packt Publishing.

▶  Text on GitHub with a CC-BY-NC-ND license
▶  Code on GitHub with a MIT license

▶  Go to Chapter 15 : Symbolic and Numerical Mathematics
▶  Get the Jupyter notebook

SymPy offers several ways to solve linear and nonlinear equations and systems of equations. Of course, these functions do not always succeed in finding closed-form exact solutions. In this case, we can fall back to numerical solvers and obtain approximate solutions.

How to do it...

1.  Let's define a few symbols:

from sympy import *
init_printing()

var('x y z a')

(x, y, z, a)

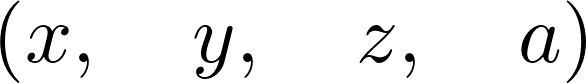
2.  We use the solve() function to solve equations (the right-hand side is 0 by default):

solve(x**2 - a, x)

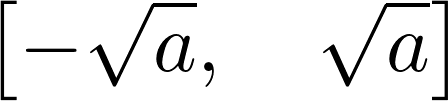
Output

3.  We can also solve inequalities. Here, we need to use the solve_univariate_inequality() function to solve this univariate inequality in the real domain:

x = Symbol('x')
solve_univariate_inequality(x**2 > 4, x)

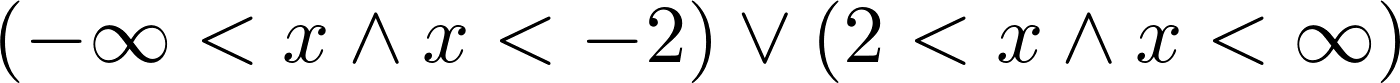
Output

4.  The solve() function also accepts systems of equations (here, a linear system):

solve([x + 2*y + 1, x - 3*y - 2], x, y)

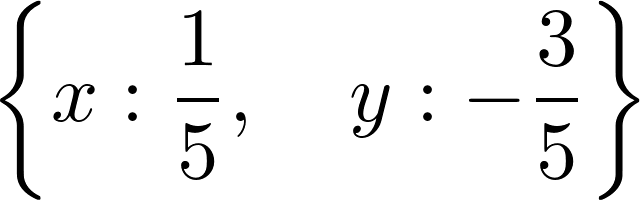
Output

5.  Nonlinear systems are also handled:

solve([x**2 + y**2 - 1, x**2 - y**2 - S(1) / 2], x, y)

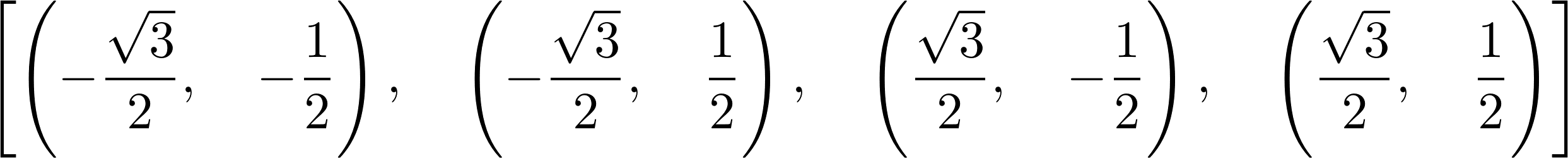
Output

6.  Singular linear systems can also be solved (here, there is an infinite number of solutions because the two equations are collinear):

solve([x + 2*y + 1, -x - 2*y - 1], x, y)

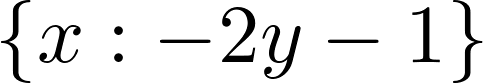
Output

7.  Now, let's solve a linear system using matrices containing symbolic variables:

var('a b c d u v')

Output

8.  We create the augmented matrix, which is the horizontal concatenation of the system's matrix with the linear coefficients and the right-hand side vector. This matrix corresponds to the following system in \(x, y\): \(ax+by=u, cx+dy=v\):

M = Matrix([[a, b, u], [c, d, v]])
M

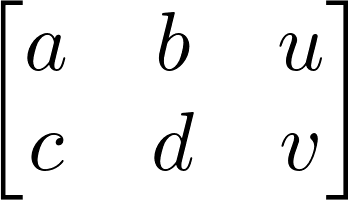
Output

solve_linear_system(M, x, y)

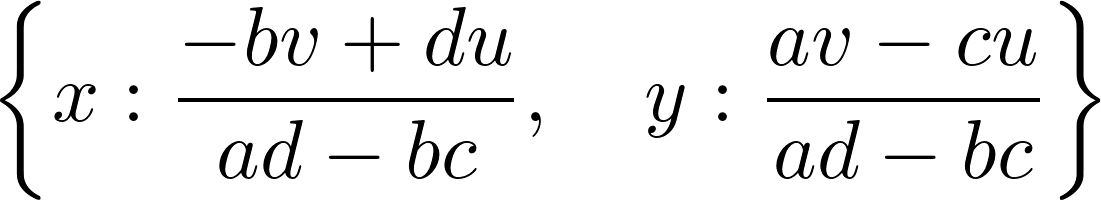
Output

9.  This system needs to be nonsingular in order to have a unique solution, which is equivalent to saying that the determinant of the system's matrix needs to be nonzero (otherwise the denominators in the preceding fractions are equal to zero):

det(M[:2, :2])

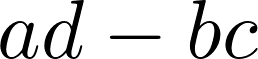
Output

There's more...

Matrix support in SymPy is quite rich; we can perform a large number of operations and decompositions (see the reference guide at http://docs.sympy.org/latest/modules/matrices/matrices.html).

Here are more references about linear algebra: